Math Journal: Geometry of annexation isn’t a completely gray area

Bloomington’s litigation over a 2017 law that stopped its effort to annex some land into the city is grinding its way towards a hearing in front of the Indiana Supreme Court.

Bloomington won a ruling from a lower court in April that found the law was unconstitutional on two grounds.

One of the State of Indiana’s allegations is that Bloomington “gerrymandered” the areas it chose for its planned annexation. For this edition of the Beacon’s Math Journal let’s not dive into the specifics of the parcels Bloomington planned to annex.

Instead, let’s take an abstract look at a geometric requirement that the state statute imposes on the possible shapes of annexed territory. The statute puts some limits on how much the shape of an annexed area can be gerrymandered.

Here’s the statutory language, describing what counts as “contiguous” territory that can be annexed:

IC 36-4-3-1.5 Contiguous territory; annexation of public highway
Sec. 1.5. (a) For purposes of this chapter, territory sought to be annexed may be considered “contiguous” only if at least one-eighth (1/8) of the aggregate external boundaries of the territory coincides with the boundaries of the annexing municipality.

The statute also describes an exception for 150-foot-wide strips, but that part will be ignored for purposes of the Math Journal.

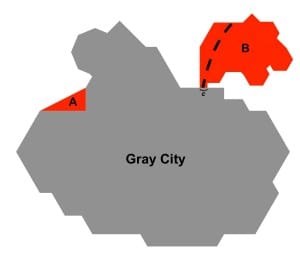
Take a look at the diagram. If the annexed area has to share at least 1/8 of its boundary with the city, then Area A in the diagram sure looks like it meets that requirement, but Area B doesn’t.

Annexation Shape Problem 1

Let’s say the sides of Area A are perfectly straight and do, in fact, form a triangle. Give a proof that Area A meets the 1/8-standard for annexation areas.

Annexation Shape Problem 2

Let’s say Area B does not meet the 1/8-standard. In other words, if the perimeter of Area B is P, and c is the length of Area B’s boundary that coincides with Gray City’s boundary, then c < 1/8*P 

What if Area B were gerrymandered into two separate areas, like the dotted line shows?

Question: Is there some way to gerrymander Area B into two areas, both of which meet the 1/8-standard? Prove your answer.

Feel free leave your answer to wither problem as a comment. If The Beacon has set up the commenting system correctly, your correct answer won’t spoil things for other people, because it will sit unseen, until it gets “approved.” After a month or so, any comments with correct answers will be approved. (If this website manages to turn a profit, maybe correct answers to future real-world math problems from The Beacon’s Math Journal will be rewarded with some kind of prize. But it’s not there, yet.)